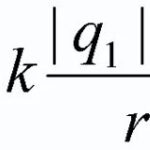Lorentz kraft og venstre hånd hersker. Bevægelse af ladede partikler i et magnetfelt

Placeret i et magnetfelt ledersom gik igennem elektricitet, påvirkes af kraften fra Ampere $F_A$ , og dens værdi kan beregnes ved hjælp af følgende formel:

$F_A=B\cdot I\cdot l\cdot sin\alpha$ (1)

hvor $jeg$ og $l$ - strømstyrke og lederlængde, $B$ - magnetisk feltinduktion, $\alfa$ - vinklen mellem retningerne af strømstyrken og magnetisk induktion. Hvorfor sker dette?

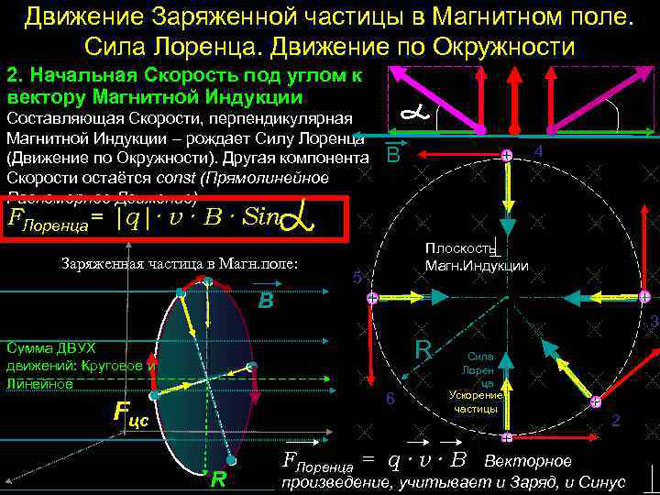
Lorentz kraft. Bevægelse af en ladet partikel i et magnetfelt.

Indhold

1 Hvad er Lorentz-kraften - bestemme hvornår den opstår, opnår formlen
2 Bestemmelse af retningen af Lorentz-kraften ved hjælp af venstrehåndsreglen
3 Bevægelse af en ladet partikel i et magnetfelt
4 Anvendelse af Lorentz-kraften i teknik

Hvad er Lorentz-kraften - bestemme hvornår den opstår, opnår formlen

Det er kendt, at elektrisk strøm er en ordnet bevægelse af ladede partikler. Det er også blevet fastslået, at hver af disse partikler under bevægelse i et magnetisk felt udsættes for påvirkning af en kraft. For at en kraft kan opstå, skal partiklen være i bevægelse.

Lorentz-kraften er den kraft, der virker på en elektrisk ladet partikel, når den bevæger sig i et magnetfelt.Dens retning er ortogonal i forhold til det plan, hvori vektorerne for partikelhastighed og magnetfeltstyrke ligger. Resultatet af Lorentz-styrkerne er Ampère-styrken. Når vi ved det, kan vi udlede en formel for Lorentz-kraften.

Den tid, det tager for partiklen at passere gennem segmentet af lederen, $t = \frac {l}{v}$ , hvor $l$ - segmentets længde, $v$ er partiklens hastighed. Den samlede ladning, der overføres i løbet af denne tid gennem lederens tværsnit, $Q = I\cdot t$ . Hvis vi her erstatter tidsværdien fra den foregående ligning, har vi

$Q = \frac {I\cdot l}{v}$ (2)

På samme tid $F_A=F_L\cdot N$ , hvor $N$ er antallet af partikler i den betragtede leder. Hvori $N = \frac {Q}{q}$ , hvor $q$ er ladningen af en partikel. Sætter værdien ind i formlen $Q$ fra (2), kan man få:

$N = \frac {I\cdot l}{v\cdot q}$

På denne måde

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

Ved at bruge (1) kan det foregående udtryk skrives som

$B\cdot I\cdot l\cdot sin\alpha = F_L\cdot \frac {I\cdot l}{v\cdot q}$

Efter sammentrækninger og overførsler fremkommer en formel til beregning af Lorentz-kraften

$F_L = q\cdot v\cdot B\cdot sin\alpha$

Da formlen er skrevet for kraftmodulet, skal den skrives som følger:

Læs også: Hvordan konverterer man forstærkere til watt og omvendt?

$F_L = |q|\cdot v\cdot B\cdot sin\alpha$ (3)

Fordi $sin\alpha = sin(180^{\circ} - \alpha)$ , så for at beregne Lorentz kraftmodulet, er det lige meget, hvor hastigheden er rettet, - i retning af strømstyrken eller imod, - og vi kan sige, at $\alfa$ er den vinkel, der dannes af partikelhastigheden og magnetiske induktionsvektorer.

At skrive en formel i vektorform vil se sådan ud:

$\vec{F_L} = q\cdot [\vec{v}\times \vec{B}]$

$[\vec{v}\ gange \vec{B}]$ er et krydsprodukt, hvis resultat er en vektor med modul lig med $v\cdot B\cdot sin\alpha$ .

Baseret på formel (3) kan vi konkludere, at Lorentz-kraften er maksimal i tilfælde af vinkelrette retninger af den elektriske strøm og det magnetiske felt, dvs. $\alpha = 90^{\circ}$ , og forsvinder, når de er parallelle ( $\alpha = 0^{\circ}$ ).

Det skal huskes, at for at opnå det korrekte kvantitative svar - for eksempel ved problemløsning - bør man bruge enhederne i SI-systemet, hvor magnetisk induktion måles i teslaer (1 T = 1 kg s⁻²·MEN⁻¹), kraft - i Newton (1 N = 1 kg m/s²), strømstyrke - i ampere, ladning i coulombs (1 C = 1 A s), længde - i meter, hastighed - i m / s.

Bestemmelse af retningen af Lorentz-kraften ved hjælp af venstrehåndsreglen

Da Lorentz-kraften manifesterer sig som Ampère-kraften i makroobjekternes verden, kan venstrehåndsreglen bruges til at bestemme dens retning.

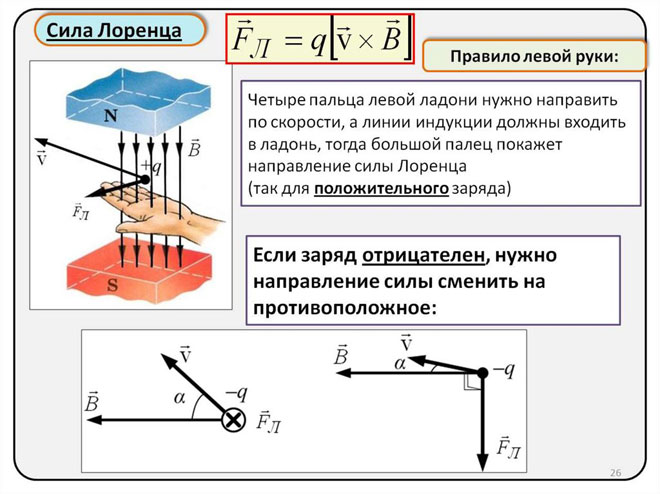
Bestemmelse af Lorentz-styrkens virkeretning i henhold til venstre hånds regel.

Du skal lægge din venstre hånd, så den åbne håndflade er vinkelret på og mod magnetfeltets linjer, fire fingre skal forlænges i retning af strømstyrken, så vil Lorentz-kraften blive rettet derhen, hvor tommelfingeren peger, hvilket skal bøjes.

Bevægelse af en ladet partikel i et magnetfelt

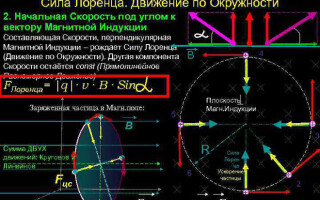
I det enkleste tilfælde, det vil sige, når vektorerne for magnetisk induktion og partikelhastighed er ortogonale, kan Lorentz-kraften, der er vinkelret på hastighedsvektoren, kun ændre sin retning. Størrelsen af hastigheden og energien vil derfor forblive uændret. Det betyder, at Lorentz-kraften virker analogt med centripetalkraften i mekanikken, og partiklen bevæger sig i en cirkel.

Læs også: Hvor mange watt er der i en kilowatt?

I overensstemmelse med Newtons II lov ( $F = m\cdot a$ ) kan vi bestemme partiklens rotationsradius:

$N = \frac {m\cdot v}{q\cdot B}$ .

Det skal bemærkes, at med en ændring i den specifikke ladning af partiklen ( $\frac {q}{m}$ ) ændres radius også.

I dette tilfælde er rotationsperioden T = $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ . Det afhænger ikke af hastigheden, hvilket betyder, at den indbyrdes position af partikler med forskellige hastigheder vil være uændret.

Bevægelse af en ladet partikel i et ensartet magnetfelt.

I et mere kompliceret tilfælde, når vinklen mellem partikelhastigheden og magnetfeltstyrken er vilkårlig, vil den bevæge sig langs en spiralformet bane - translationelt på grund af hastighedskomponenten rettet parallelt med feltet, og langs cirklen under påvirkning af dens vinkelret komponent.

Anvendelse af Lorentz-kraften i teknik

Kinescope

Kinescope, som stod indtil for nylig, da det blev erstattet af en LCD (flad) skærm, i ethvert tv-apparat, kunne ikke fungere uden Lorentz-styrken. For at danne et tv-raster på skærmen ud fra en snæver strøm af elektroner, bruges afbøjningsspoler, hvor der skabes et lineært skiftende magnetfelt. De vandrette spoler flytter elektronstrålen fra venstre mod højre og returnerer den tilbage, personalespolerne er ansvarlige for den lodrette bevægelse, og bevæger strålen, der løber vandret fra top til bund. Samme princip bruges i oscilloskoper - enheder, der bruges til at studere elektrisk vekselspænding.

massespektrograf

En massespektrograf er en enhed, der bruger afhængigheden af en ladet partikels rotationsradius af dens specifikke ladning. Princippet for dets funktion er som følger:

Kilden til ladede partikler, som tager fart ved hjælp af et kunstigt skabt elektrisk felt, placeres i et vakuumkammer for at udelukke påvirkning af luftmolekyler. Partikler flyver ud af kilden og, efter at have passeret langs en cirkelbue, rammer den fotografiske plade og efterlader spor på den. Afhængigt af den specifikke ladning ændres banens radius og dermed anslagspunktet. Denne radius er nem at måle, og ved at vide det, kan du beregne massen af partiklen. Ved hjælp af en massespektrograf blev for eksempel månejordens sammensætning undersøgt.

Læs også: Hvilke erhverv er relateret til elektricitet

Cyklotron

Periodens uafhængighed, og dermed frekvensen af rotation af en ladet partikel fra dens hastighed i nærvær af et magnetfelt, bruges i en enhed kaldet en cyklotron og designet til at accelerere partikler til høje hastigheder. En cyklotron er to hule metal halvcylindre - en dee (i form ligner hver af dem det latinske bogstav D) placeret med lige sider mod hinanden på kort afstand.

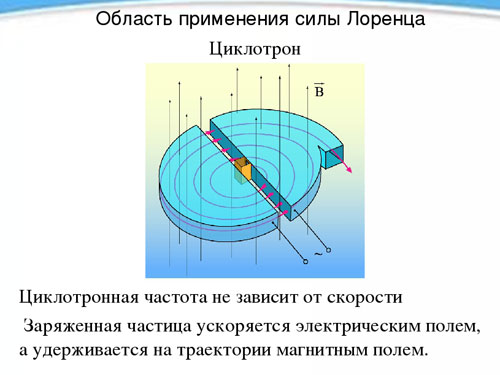
Cyclotron - anvendelse af Lorentz-kraften.

Deerne placeres i et konstant ensartet magnetfelt, og der skabes et vekslende elektrisk felt mellem dem, hvis frekvens er lig med partiklens rotationsfrekvens, bestemt af magnetfeltets styrke og specifik ladning. Ved at blive to gange i løbet af rotationsperioden (under overgangen fra en dee til en anden) under påvirkning af et elektrisk felt, accelererer partiklen hver gang, øger banens radius og på et bestemt tidspunkt, efter at have opnået den ønskede hastighed, flyver ud af enheden gennem hullet. På denne måde kan en proton accelereres til en energi på 20 MeV (megaelektronvolt).

Magnetron

En enhed kaldet en magnetron, som er installeret i hver mikrobølgeovn, er en anden repræsentant for enheder, der bruger Lorentz-styrken. Magnetronen bruges til at skabe et kraftigt mikrobølgefelt, som opvarmer det indre rum i ovnen, hvor maden placeres. Magneterne inkluderet i dens sammensætning korrigerer banen for elektronernes bevægelse inde i enheden.

Jordens magnetfelt

Og i naturen spiller Lorentz-kraften en ekstremt vigtig rolle for menneskeheden. Dens tilstedeværelse gør det muligt for Jordens magnetfelt at beskytte mennesker mod den dødelige ioniserende stråling fra rummet. Feltet tillader ikke ladede partikler at bombardere planetens overflade, hvilket tvinger dem til at ændre retning.

Lignende artikler: